無限面のサイコロは球なのか？

気になりますよね．

この記事は ICT Advent Calendar 2015 の 25 日目の記事です．

まえがき

前掲した Google Docs のページ，半分以上誰なのか分からないので自分が老害である事実をより一層噛み締めているなとりうむです．久留米高専プロラボ部の OB で，前の前の前の部長をしてました．今週沖縄行ってました．コーレーグース美味しい．

無限面のサイコロ？

偉大なるまるさ先輩のブログのタイトルです．無限面のサイコロってなんでしょうね．とりあえずサイコロと聞いて思い浮かべる図形を wikipedia から拝借して来ました．

f:id:natrium11321:20151206212820g:plain:w150 f:id:natrium11321:20151206212349g:plain:w150 f:id:natrium11321:20151206212542g:plain:w150

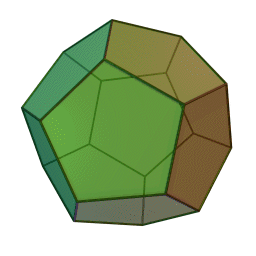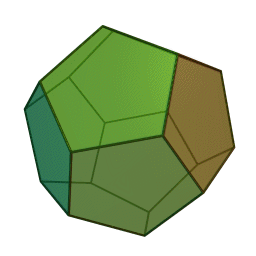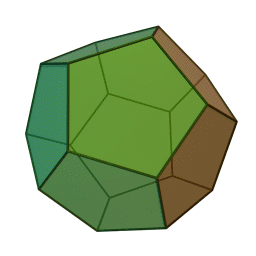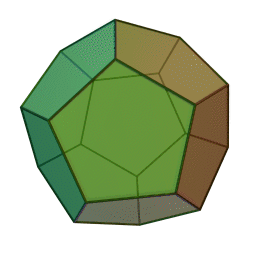
左から順に正四面体，正六面体，正八面体，正十二面体，正二十面体です．確かに面*1の数が増えてくるとだんだん球に近いような形になってるっぽいオーラが出ています．この調子で面の数を無限まで増やしていけばきっと球に・・・？

無限は怖い

話はそう簡単ではありません．基本的に数学で無限というのはとても怖い単語で，その手の人が聞いたら「加算？非加算？あ，連続体仮説認めない人？」とか「超準解析」とか「選択公理反対！」とか「ℵ」とか，このような反応が帰ってきます．怖いですね．ちなみに僕もここ最近有限の数しか扱ってないので，安易に無限を扱うのが怖いです．この文章にマスカリ飛んできそう．;;(∩´﹏`∩);;

しかしここで足を止めてしまってはいけません．例え怖い人達にマサカリを投げられようとも，サイコロに因縁のある僕らは「無限面のサイコロ」の正体を暴かなければならないのです．ICT Advent Calendar とはそういうものだったはず．

サイコロを定義しよう

サイコロという概念をきちんと定義しないとこの議論は出来ません．ある図形がサイコロであると呼ぶのにふさわしい性質は何でしょうか．まず，サイコロである以上，その図形を振ることが出来なければ意味がありません．サイコロは数えるものでも並べるものでもないですね．次に，振った結果として「目」が出る必要があります．つまり，どの面が出たのかがきちんと分かる必要があります．

以上の要求を踏まえて，この文章では以下を満たすものをサイコロ (dice) と呼ぶことにします．

定義（サイコロ）

$\mathbb{R}^n$ の部分集合 $S \subseteq \mathbb{R}^n$ は以下の条件を満たすとき，サイコロであるという．

$S$ は $n$ 次元凸多面体である．但し $n$ 次元凸多面体とは， $n=0$ の時は単元集合であり， $n \geq 1$ の時はその境界が加算個の $n-1$ 次元凸多面体の和で書けるような $n$ 次元閉凸集合を表す．

$S$ は空でない*2．

$S$ は有界である．

難しそうな単語がいっぱい出てきました．これを口語訳するとこうなります．

定義（サイコロ）

$n$ 次元空間の図形 $S$ は以下の条件を満たすとき，サイコロであるという．

$S$ は凹みのない $n$ 次元の図形で，面が数えられるくらいしかなくて，しかもその全ての面とか辺とかは全て真っ直ぐであり，曲がっていない．

$S$ の実体は存在する．

$S$ は無限に大きくない．

この定義のキモチを考えてみましょう．条件が 3 つありますが，本質的な条件は 1 のみです．条件 1 の前半は「凹みがない」ことを言っています．確かに凹んでいる図形は，凹んでいる部分の面が地面に接することがないため，サイコロとして使えそうにありません．一方後半はすべての面が安定してきちんと地面に接することが出来ることを保証しています．確かにこの条件はサイコロとして必要っぽいです．条件 2 と 3 は，虚空を指してここにサイコロがあると言いはったり，逆にこの宇宙全体*3が実はサイコロだと主張したり，そんな感じの変な図形を除外している感じです．

逆に，上記の定義に当てはまる図形は赤子が泣こうが全てサイコロです．

どんなものがサイコロなんだろう

例 1. 点（0 次元）

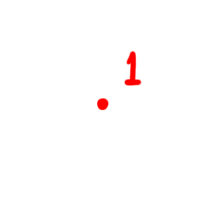
点は 0 次元空間の（唯一の）サイコロです．数式で書くと $\{0\}$ です．ちなみにこのサイコロ，常に 1 の目しか出しません．たまげたなあ．

例 2. 線分（1 次元）

1 次元空間のサイコロは（長さと位置の違いを除いて）線分しかありません．数式で書くと $[0, 1]$ みたいな感じです．このサイコロは 1 の目か 2 の目を出してくれます．優秀．

例 3. 正方形（2 次元）

空間の次元が 2 まで上がると一気に色々なサイコロを考えることが出来るようになりますが，その中で最も初等的なのがこれです． $[0, 1]^2$ みたいにかけます．1 の目から 4 の目まで当確率で出してくれるし，向かい合う目の合計は全て 5 だし，優秀そうなサイコロです．

例 4. 立方体（3 次元）

僕らが最もよく知っている 6 面サイコロです．謎の安心感があります．

例 5. 正八胞体（4 次元）

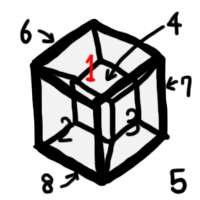
1 から 8 までの面（といっても各面は通常の意味での立方体ですが）があります．

球は無限面のサイコロなのか？

本題に戻りましょう．（3 次元の）球は無限面のサイコロと言えるのでしょうか．答えは残念ながら No です*4．何故なら球の面（境界）は球面ですが，球面はまっすぐな平面を幾つか切り貼りして作ることが出来ない（凸多面体ではない）からです．そもそも球，振っても何の目が出たか分かんないし…………

じゃあ無限面のサイコロってあるの？

あります．

例 6. 無限面のサイコロ 1（2 次元）

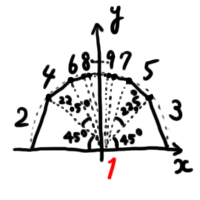
なんかやばそうな平面図形が出てきましたが，これは何をしているかというと，単位円の上半分に頂点を沢山置いて，それらを辺で結んでいるだけです． $y$ 軸に近いほどいっぱい頂点を置いています．多分 $y$ 軸と成す角度が $2^{-n}\pi$ ( $n \in \mathbb{N}$ ) くらいの所が頂点になっています．確かにこいつは辺（2 次元図形の面）が無限にあります．しかも，「数えられる量」の辺を組み合わせることで作られています（無限個あるけど，全部長さは 0 じゃないし，1, 2, … って数えられる）．面によって出やすさが異なりますが，サイコロの定義を満たしているので，これは正真正銘のサイコロです！ちゃんと何の目が出たか分かります（地面に接した面を「出た目」とする）．冬休み暇な人はそれぞれの目の出る確率を計算してみてください．

例 7. 無限面のサイコロ 2（無限次元）

次元を無限まで上げて， $[0, 1] \times [0, 1] \times \cdots$ ってすればいいと思うんですが，無限は怖いので言及を避けます*5 ;;(∩´﹏`∩);;

結論

普通の 6 面サイコロを普通に使おう．

*1:さっきから「めん」で変換すると真っ先に「麺」が出てくる…

*2:この定義だと 1. から $S$ の非空性が言えるので実は不要．空集合の次元は $-1$ でありこれは $n$ と異なる．

*3:宇宙全体が非有界なのかという議論はここでは置いておきます．

*4:もちろん，上のサイコロの定義に従うと，という話なので，定義を変えればサイコロって言い張ることも出来ます！

*5:加算無限次元の線型空間というものを考えることは出来るはずで，凸性は well-defined だと思うんですが境界演算子とかがどうなるかよく分からない．書いた定義をそのまま拡張すると「無限次元凸多面体」の定義が循環して全ての閉凸集合が凸多面体になっちゃう気がするぞい．幾何怖い;;(∩´﹏`∩);;